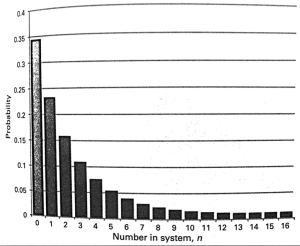
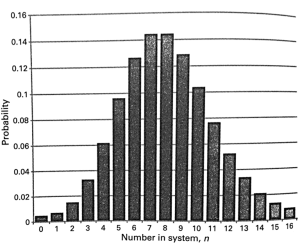
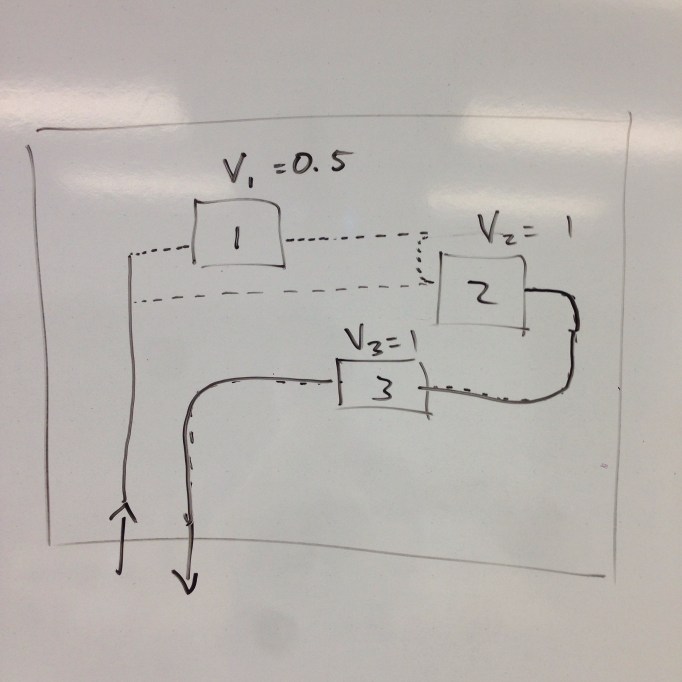
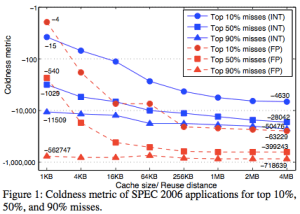
The Working-Set models motivates to design adaptive memory management policies based on analytic program behaviors. A program’s working set is the smallest subset of its pages that have to reside in memory provided the program operates at a desired level of efficiency.
Consider a program with n pages, constituting the set N = 1, 2, . . . , n, the reference string is a sequence of pages, i.e. p = r1r2 …rt …, each rt being in N. rt = i denotes page i is referenced at the t-th reference. A locality is a subset of its mostly recent referenced pages. A reference missing of page is defined as a referenced page is not in the locality set. A locality set is a working-set.
Next let’s define working set, missing-page rate and inter-reference interval precisely.
A Working-set W(t,T) is the set at time t of distinct pages referenced in the time range [t − T + 1, t]. T is window size. Then we can compute the average number of distinct pages of some window size T.
s(T) = \lim_{k\rightarrow \infty} \frac{1}{k}\sum_{t=1}^{k}w(t,T)
where w(t,T) is the size of W(t,T) set.
The missing-page rate m(T) measures the number of page references per unit time not in the working set. ∆(t,T) = 1 if rt+1 is not in W(t,T), 0 otherwise.
m(T) = \lim_{k\rightarrow \infty} \frac{1}{k}\sum_{t=0}^{k-1}\Delta (t,T)
In a reference string r1r2 . . . rt . . ., two successive references to pages i occur at times t and t + xi, we call xi an inter-reference interval for page i. The inter-reference interval distribution of page i is defined as
F_i(x) = \lim_{k\rightarrow \infty} \frac{{\textit{no. }}x_i \in r_1\dots r_k \textit{ with } x_i \le x}{\textit{ no. }x_i \in r_1\dots r_k }
Based on three assumptions related with locality, 1) reference strings are endless, 2) the stochastic mechanism underlying the generation of a reference string is stationary, and 3) references are asymptotically uncorrelated, the working-set theory has the relationships among average working- set size, missing-page rate and the inter-reference-interval distribution can be derived from both time-average statistics and window-average statistics.