Shuchang Zhou proposed a efficient algorithm to calculating the hit probability for cache with random replacement policy.
How much one cache can influence performance are often evaluated by running a cache simulator by collected traces. Different associativities, sizes and replacement policies will lead to different result. But for one special cache with random replacement policies, single round simulation can only gives one possible result of performance because of the randomness. So we have to run the simulation multiple times to get a average performance which is very inefficiency.
Based on this observation, they came up with a efficient way to calculate hit probability of each memory access by using expectation, which can be used to derive miss ratio.
Foundation:
The trace of the accessed sequence (cache lines) is:
a0, a1, a2, …, aN.
The miss event of time i is Xi. if a miss event happens at i, then Xi = 1, else Xi = 0.
X0, X1, X2, … XN.
So the hit event will be 1-Xi at time i.
Assume k is the time when the reuse window starts, the number of misses since k to time i will be Zi.
If the reuse window exists,
Zi = sum(Xl), ( k+1<=l<= i-1 )
Else,
Zi = infinite
The expectation will be the following according to the linearity of expectation,
E(Zi) = sum( E(Xl) ) , ( k+1<=l<= i-1 ) or infinite
With the definition number of misses Zi, E(Xi) can be defined as:
E(Xi) = 1 – E( (1-1/M)^Zi ), M is the cache size
When M is very large,
E(Xi) ~ 1-(1-1/M)^E(Zi)
Proof:
if Zi == infinite:
1-(1-1/M)^E(Zi) = 1 – E( (1-1/M)^Zi ) = 0
Else:
Then they proposed two algorithms to calculate E(Zi ) efficiently from E(Xi) and compared the results with average 5, 50, 500 round naive simulation which proves their method has less error.
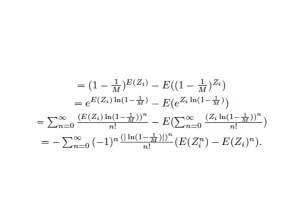
Random replacement in cache has been used in various caching models. A often neglected issue is the non-determinism of random replacement. This paper solves the problem with a one-pass solution to compute the expected miss ratio.