Better utilization on cache usually results in better performance, but this paper shows in NUMA architecture, memory accesses balance is more important than locality on local LLC.
NUMA
NUMA machines are consist by more than 2 sockets, each of them has independent memory controller and cache. Form a socket’s perspective, its own cache/memory are defined as local cache/memory, and others are remote ones. Sockets transform data through interconnection bus. They access data with following rules:
1.If datum is not in local cache, turns 2
2.Require datum from remote cache, if there is no datum in that cache, turns 3
*3.read data from remote memory
The architecture and overheads are showed with followed figure.
Issues
Remote access latency has a higher overhead, thus an intuitively thinking is higher local cache access ratio will result in better performance. But in this paper author found that, when serious congestion comes up, latency of accessing remote memory will incredibly increasing, says from 300 to 1200 cycles.
They show this issues by firstly show the overhead of congestion, by comparing two different memory placement scenario. The first one is First touch scenario(F), “the default policy where the memory pages are placed on the node where they are first accessed”. The second one is Interleaving (I) – “where memory pages are spread evenly across all nodes.” These two scenarios are showed in Fig 3 of that paper. It is obviously that F has better cache
With experiments on NAS, PARSEC and map/reduce Metis suits, authors shows that in 9 of 20 benchmarks, F is the better one and only in 5 benchmarks, I is better. Which is also showed in Fig 2(b). But, in 3 programs, I gets more than 35% better performance than F. In other side, all of F get not more than 30% better performance than I except one.
And then they showed two cases study in Table 1 that , even some program has better local access ratio(25% vs 32%), but its higher memory latency(465 vs 660) also regrades the performance.
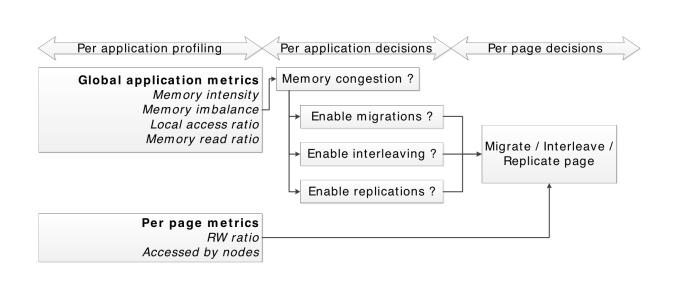
Approach
They use four strategies to reduce congestion and improve locality:
1.Page relocation : “when we re-locate the physical page to the same node as the thread that accesses it”
2.Page replication: “placing a copy of a page on several memory nodes”
3.Page interleaving : “evenly distributing physical pages across nodes.”
*4.Thread clustering : “co-locating threads that share data on the same node”
The workflow is showed in followed figure: